Найди значение выражения 18 + 44.
Ответ: 62.
Найди значение выражения (19 + 22) · 2 + 9.
Ответ: 91.
Рассмотри рисунок и ответь на вопрос: сколько рублей сдачи получит покупатель, расплатившийся за одну лилию и одну розу купюрой в 500 руб.? Запиши решение и ответ.
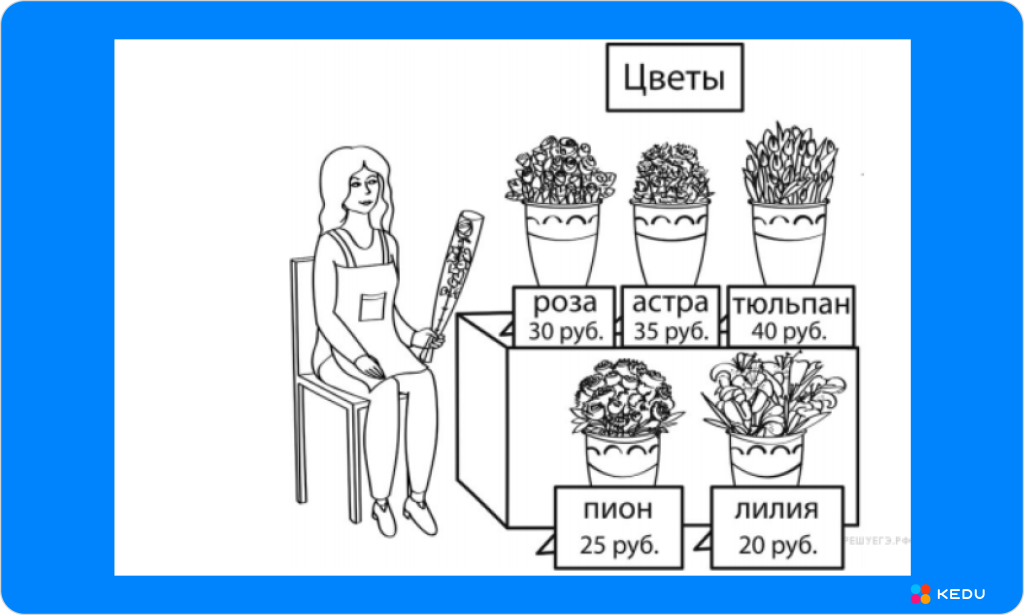
Источник: kedu.ru
Ответ: 450 руб.
Позавчера был понедельник. Какой день недели будет завтра?
Пояснение.
Позавчера был понедельник. Вчера был вторник. Сегодня среда. Завтра четверг.
Ответ: четверг.
На клетчатом поле со стороной клетки 1 см изображён прямоугольник. Найди периметр этого прямоугольника.
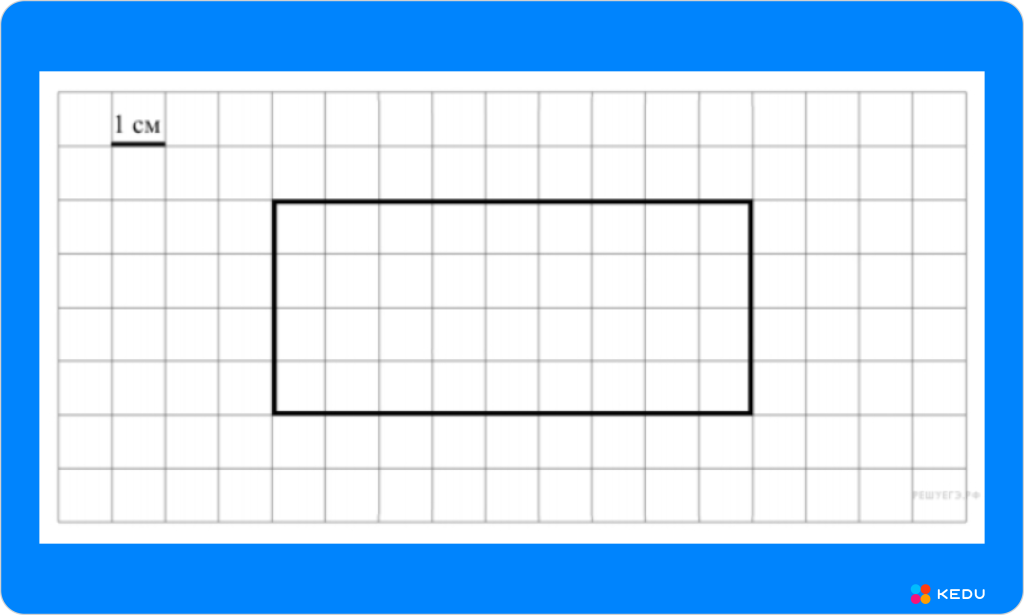
Источник: kedu.ru
Пояснение.
Периметр прямоугольника равен: см.
Ответ: 26.
Лист бумаги расчерчен на клетки со стороной 1 см. Нарисуй по клеткам прямоугольник, который содержит все отмеченные клетки и имеет периметр 16 см.
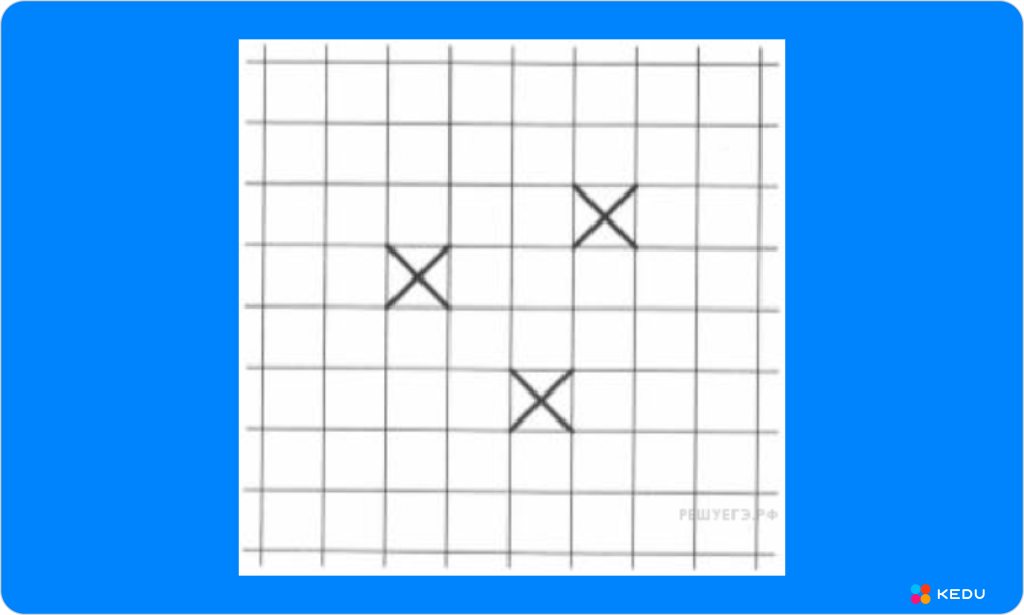
Источник: kedu.ru
Пояснение.
Периметр 16 могут иметь прямоугольники со сторонами 1 и 7, 2 и 6, 3 и 5, 4 и 4. Подходит под чертеж прямоугольник со сторонами, 4 и 4:
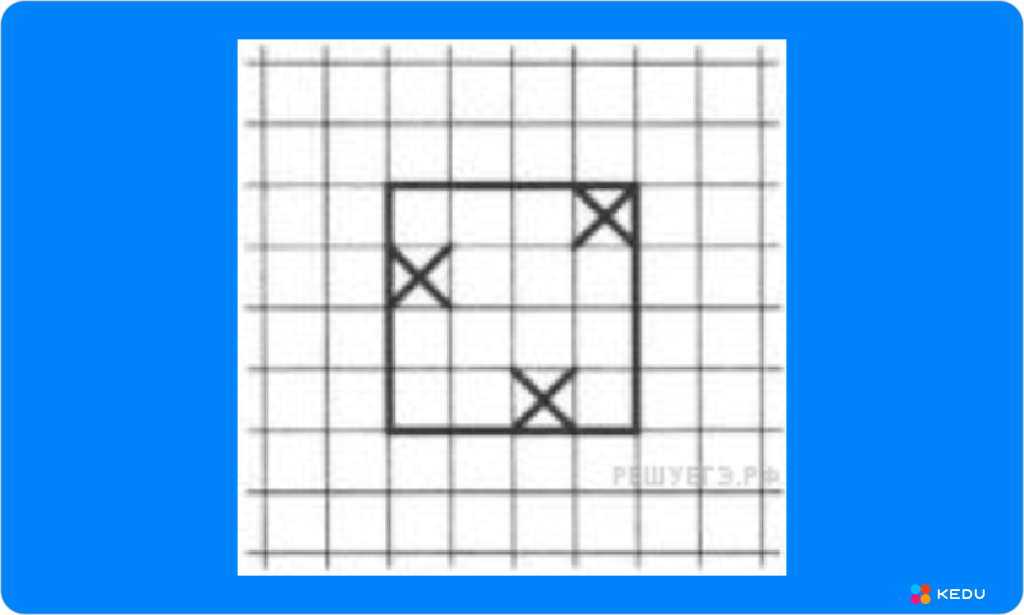
Источник: kedu.ru
В таблице приведены данные о численности населения трёх областей России в разные годы (в тыс. человек). Используя эти данные, ответь на вопросы.
| Область | Численность населения | ||||
| 1970 г. | 1979 г. | 1990 г. | 2000 г. | 2010 г. | |
| Астраханская | 1400 | 1467 | 1575 | 1390 | 1230 |
| Мурманская | 800 | 965 | 1191 | 941 | 795 |
| Калининградская | 730 | 807 | 881 | 959 | 940 |
В каком году численность населения в Астраханской области была наибольшей?
Пояснение.
Из таблицы видно, что численность населения в Астраханской области была наибольшей в 1990 г.
Ответ: 1990.
В таблице приведены данные о численности населения трёх городов России в разные годы (в тыс. человек). Используя эти данные, ответь на вопросы.
| Город | Численность населения | ||||
| 1970 г. | 1982 г. | 1990 г. | 2000 г. | 2010 г. | |
| Екатеринбург | 1025 | 1250 | 1304 | 1264 | 1350 |
| Ростов-на-Дону | 790 | 966 | 1013 | 1001 | 1090 |
| Казань | 780 | 1023 | 1094 | 1092 | 1150 |
В каком городе численность населения за период с 1970 по 2010 год выросла больше, чем в двух других?
Пояснение.
Найдем разницу в численности населения в каждом из городов:
- Екатеринбург: 1350 - 1025 = 325.
- Ростов-на-Дону: 1090 - 790 = 300.
- Казань: 1150 - 780 = 370.
Численность населения за период с 1970 по 2010 год выросла больше в Казани.
Ответ: в Казани.
Найди значение выражения 42 · 8 − 33000 : 550.
Ответ: 276.
Масса двенадцати одинаковых коробок с бананами равна 240 кг. Масса пустой коробки — 500 г. Чему равна масса бананов в одной коробке? Запиши решение и ответ.
Пояснение.
- 240 : 12 = 20 (кг) — масса одной коробки с бананами.
- 20 кг − 500 г = 19 кг 500 г — масса бананов в одной коробке.
Ответ: 19 кг 500 г.
Машины на стоянке стоят в семь рядов: в первом ряду четыре машины, во втором три, в третьем снова четыре, в четвёртом снова три и так далее. Сколько на стоянке рядов по три машины?
Ответ: 3.
Рассмотри рисунок и установи закономерность.

Источник: kedu.ru
Выбери фигуру, которую надо поставить вместо вопросительного знака. Запиши её номер.
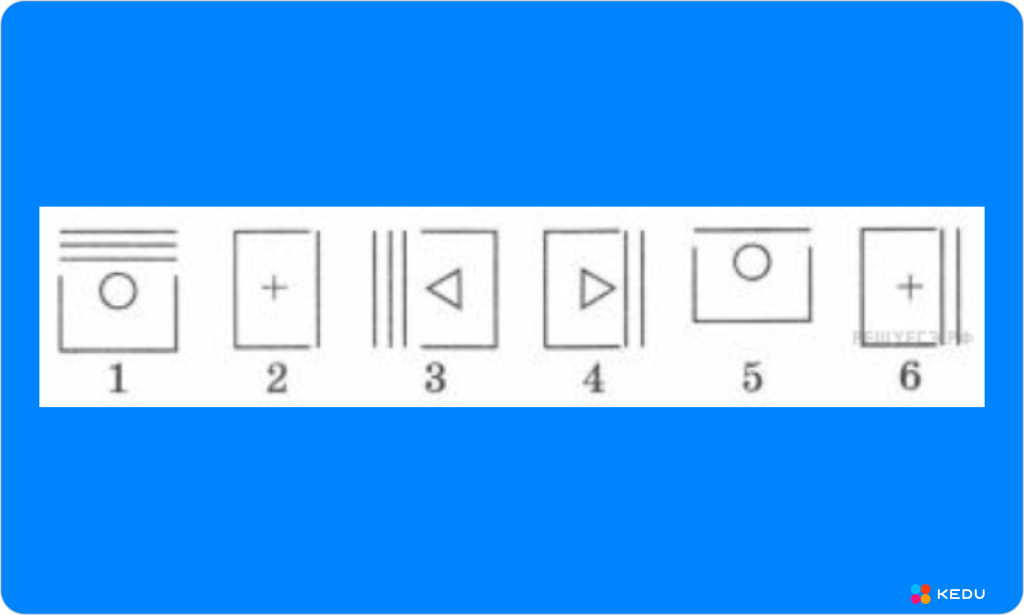
Источник: kedu.ru
Пояснение.
Фигура должна быть повернута вправо, внутри нее должен быть крестик и сбоку должно быть две линии. Следовательно, это фигура номер 6.
Ответ: 6.
На столбе висел знак (см. рис. 1). Верхний болт, державший знак, отвалился, и знак перевернулся. Нарисуй, как будет выглядеть знак (рис. 2).
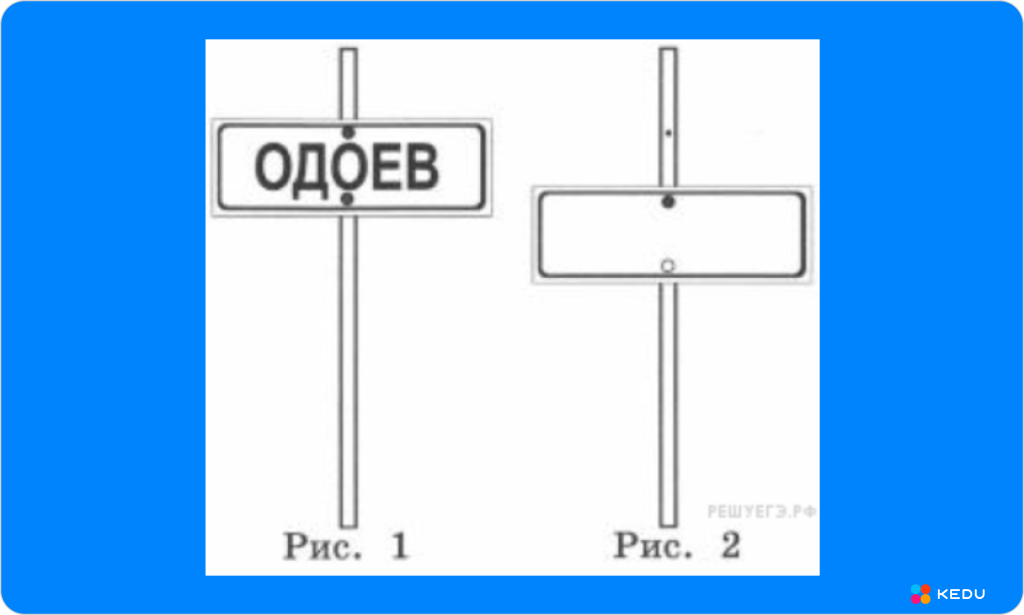
Источник: kedu.ru
Пояснение.
Знак будет выглядеть следующим образом:
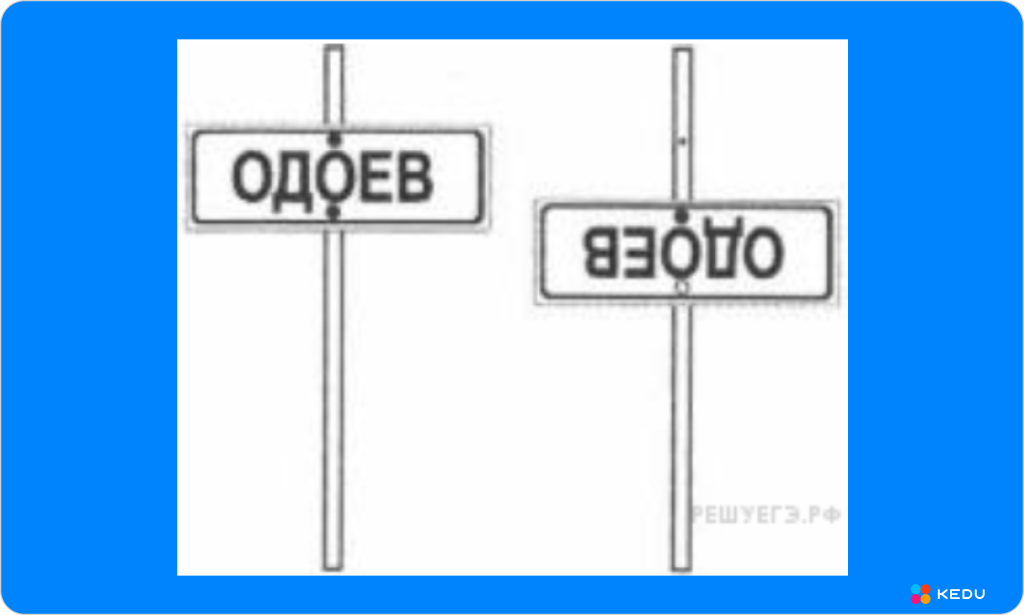
Источник: kedu.ru
В шахматном кружке проводился турнир в средней группе обучающихся, в рамках которого каждый участник играл с каждым другим по две партии (одну белыми фигурами, а другую — чёрными). За победу начислялось 2 очка, за ничью — 1 очко, за поражение 0 очков. Всего в турнире участвовало пять ребят. Игорь занял второе место, набрав больше очков, чем Руслан, Люда и Вова вместе взятые. Сколько очков набрала Оля, занявшая первое место?
Пояснение.
Всего было сыграно 20 партий. В 20 партиях разыгрывалось 40 очков. Предположим, что Оля выиграла все партии, то есть набрала 16 очков. В таком случае Игорь может набрать максимально 12 очков (2 проигрыша Оле). Получается, что Руслан, Люда и Вова в сумме набрали 40 − 16 − 12 = 12 очков, что противоречит условию. Предположим, что Оля однажды сыграла вничью с Игорем, набрав таким образом 15 очков. Следовательно, Игорь максимально может набрать 13 очков, а это значит, что остальные ребята набрали в сумме 12 очков, что и является решением. В остальных случаях условия задачи не выполняются. В таблице представлены возможные ситуации.
| Оля | Игорь | Остальные ребята |
| 16 | 12 | 12 |
| 15 | 13 | 12 |
| 14 | 14 | 12 |
Ответ: 15.












